I want to use \sum to express 1 3 5 7 2n 1 Can I?Test the convergence of the series \(\Large \sum\limits_{n=1}^{\infty}\frac{135(2n1)}{2462n}x^{n},x\ge 0\)Click here👆to get an answer to your question ️ Prove n^n > 135 , (2n 1)

Sum Of Squares Of Odd Numbers 1 2 3 2 5 2 2n 1 2 Derivation Formula Prmo Rmo Iit Youtube
1+3+5+7+9+...+2n-1 sum formula
1+3+5+7+9+...+2n-1 sum formula-The next term of the sequence, ie the (n1)th term 1, 3, 5, , (2n1) which is summed is (2n1), now with n=1 the relationship, 1 3 5 (2n1) = n^2 (1) holds obviously since both sides are 1 Now say (1) holds for n = k for some positive integer k, then, 1 3 5 (2k1) = k^2 add the next term (2k1) to both sides, then;Find the sum of the terms of the arithmetic sequence 1, 7, 13, 19, , 109, n = 19 asked Feb 19, 14 in ALGEBRA 1 by johnkelly Apprentice sequenceseries



Find The Sum Of Series Upto N Terms 2n 1 2n 1 3 2n 1 2n
The six trigonometric functions can be defined as coordinate values of points on the Euclidean plane that are related to the unit circle, which is the circle of radius one centered at the origin O of this coordinate system While rightangled triangle definitions allows for the definition of the trigonometric functions for angles between 0 and radian (90°), the unit circle definitions allowIn this section we will discuss using the Ratio Test to determine if an infinite series converges absolutely or diverges The Ratio Test can be used on any series, but unfortunately will not always yield a conclusive answer as to whether a series will converge absolutely or diverge A proof of the Ratio Test is also givenOr what methods can I use to express this sequence?
Algebra Fundamentals Supercharge your algebraic intuition and problem solving skills!#SumofSquaresOfOddNumbers #SumOfSquares #OddNumbers #IIT #JEE #NMTC #NTSE #PERMO #RMO #INMOFormula to find the sum of squares of first n odd numbersLink to tBefore progressing further, we should know that series (2n1) will have a sum of n 2, and the series 1 2 2 2 3 2 4 2 n 2 will have a sum of i 2 = Program to illustrate the working of our code Example Live Demo
Uncategorized No Comments SolvedExercise 11 Prove Sum First N Odd Integers N2 1 3 5 2n 1 N2 Exercise 12 Prove N Q Answer to Exercise 11Weekly Subscription $199 USD per week until cancelled Monthly Subscription $499 USD per month until cancelled Annual Subscription $2999 USD per year until cancelledThe nth term of this sequence is 2n 1 In general, the nth term of an arithmetic progression, with first term a and common difference d, is a (n 1)d So for the sequence 3, 5, 7, 9,



Sum Of The First N Odd Numbers Is N 2 Mathematics Stack Exchange



Terms 25 Find The Sum Of The Following Series Up To 11 221 23
You have to be very careful with power series They all have a range of values for which they work Consider the power series P = 1 x x^2 x^3 x^4 x^5 x^6 \pm \cdots This is a3 MATHEMATICAL INDUCTION Which shows 5(n 1) 5 (n 1)2By the principle of mathematical induction it follows that 5n 5 n2 for all integers n 6 Discussion In Example 341, the predicate, P(n), is 5n5 n2, and the universe of discourse is the set of integers n 6Uncategorized No Comments SolvedExercise 11 Prove Sum First N Odd Integers N2 1 3 5 2n 1 N2 Exercise 12 Prove N Q Answer to Exercise 11



Solved Here Are A Couplc Of Formulas 2i 1 1 3 5 Chegg Com


What Is The Sum Of The Series 1 1 3 5 1 3 5 7 1 5 7 9 Up To N Terms Quora
The sum of the first n numbers of an arithmetic sequence can be derived from this formula The values of a, d and n are a = 1 (the first term)The value of `i^(135(2n1))` is_____ Doubtnut is better on App Paiye sabhi sawalon ka Video solution sirf photo khinch kar Open App Continue with Mobile Browser Books If the sum terms of the series then find the value of 1147 16k LIKES 321k VIEWSThe sequence of double factorials for odd n = 1, 3, 5, 7, 9, starts as 1, 3, 15, 105, 945, , , (sequence A in the OEIS) The term odd factorial is sometimes used for the double factorial of an odd number Additional finite sum expansions of congruences for the


To Solve The Sum Of The Series 1 3 5 2n 1 Where K 1 To N Nth Term In The Series Graphically By Jimmy Lo Medium



1 2 3 4 Wikipedia
Actually for the first question tex\sum^{\infty}_{n=1} \frac{n!}{135(2n1)}/tex you made a mistake while simplifying tex\frac{s_{n1}}{s_{n}} = \frac{(nBefore progressing further, we should know that series (2n1) will have a sum of n 2, and the series 1 2 2 2 3 2 4 2 n 2 will have a sum of i 2 = Program to illustrate the working of our code Example Live DemoOr what methods can I use to express this sequence?



Ex 4 1 7 Prove 1 3 3 5 5 7 2n 1 2n 1 Class 11


What Is The Summation Of The Series 1 3 6 10 15 Quora
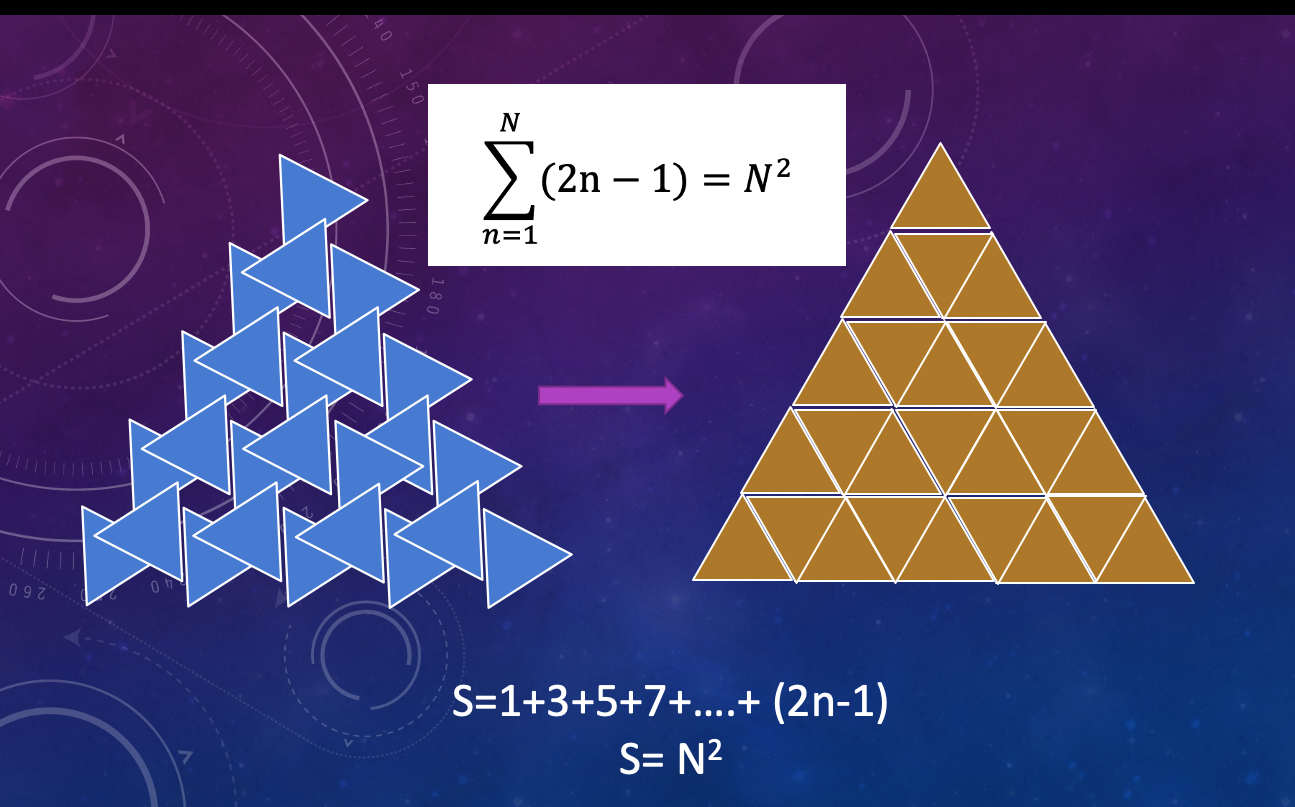
When n = 1, we have (2(1) 1) = 1 2, so the statement holds for n = 1 Step 2 Assume that the equation is true for n, and prove that the equation is true for n 1 Assume 1 3 5 (2n 1) = n 2Find the first five terms of the sequence with an = 5 2n Enter them in order (a1, a2, a3, a4, a5) Find the geometric mean of 1/8 and 1/18 Find the first five terms of the sequence with a1 = 9 and an = 2an1 3 Enter them in order (a1, a2, a3, a4, a5) Find the sum S27 for the geometric series 7 14 28 56 Find the first three terms of the geometric sequence with a6 = 128 and a11This basically tells me that the arithmetic sequence is 2n1 To verify, simply plug in the 1st term (n=0) and you'll get 1 Plug in the 2nd term (n=1) you'll get 3, if I let n=2 I get 5, etc


What Is The Sum Of The Series 1 1 3 5 1 3 5 7 1 5 7 9 Up To N Terms Quora
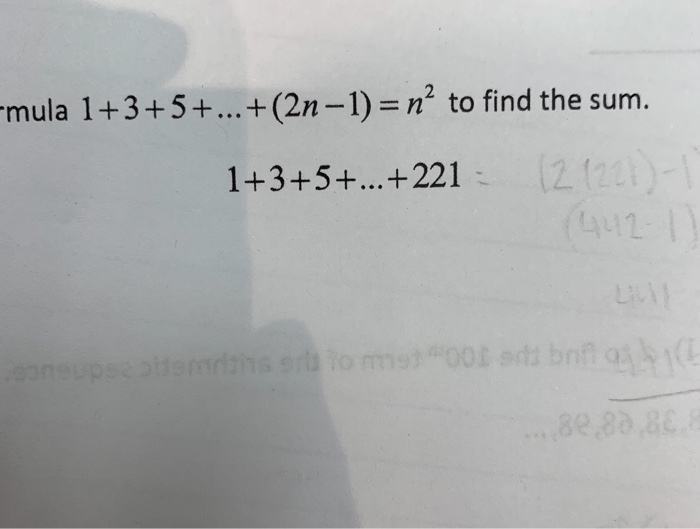


Solved Mula 1 3 5 2n 1 N To Find The Sum 1 3 5 Chegg Com
(For example 1, 4, 9, 16, 25 and 36 are all perfect squares) Prove by induction that the sum 1 3 5 7 2n1 (ie the sum of the first n odd integers) is always a perfect square 3 Show that any 2 n x 2 n board with one square deleted can be covered by Triominoes(2n1) = 3 5 7 9 = 24 And we can use other letters, here we use i and sum up i × (i1), going from 1 to 3 3In this section we will discuss using the Ratio Test to determine if an infinite series converges absolutely or diverges The Ratio Test can be used on any series, but unfortunately will not always yield a conclusive answer as to whether a series will converge absolutely or diverge A proof of the Ratio Test is also given



Ex 4 1 7 Prove 1 3 3 5 5 7 2n 1 2n 1 Class 11



Rd Sharma Solutions For Class 11 Chapter 19 Arithmetic Progressions Download Free Pdf
1;3;1 or 1;4;3 would both indicate di erent rising diagonals of the triangle We now go on to relate the rising diagonals to the Fibonacci numbers Theorem 1 The sum of the numbers along a rising diagonal in Pascal's triangle is a Fibonacci numberThis is an arithmetic series with a=1 and d=2 The Nth term is a(N1)d=12(N1)=2N1=2n1 so N=(n1) The sum is (N/2)(2a(N1)d)=N^2=(n1)^2 Check n=3, 1357=16=(31)^2 so OK\begin{aligned} \frac { \sum _{ i=1 }^{ 17 }{ { i }^{ 2 } } }{ 1009\cdot 1345 } &=\frac {\ \ \frac { 17(171)(2\cdot 171) }{ 3!



5 1 Sequences And Summation Notation T



Practice For Exam 2 Math 3410
The Sum Of The First N Terms Of The Series 1 Square 2 2 Square Is Where N Is Even When N Is Odd The Sum Is The Sum Of The Infinite Terms Of The Following Series 1 Pl 4 By 5 Pl 7 By 5 Sq Plus Will Be The Sum Of The N Terms Of The Series 12 By 1 3 Plus 22 By 3 5 Plus 32 By 5 7 Plus N2 By 2n 1 2n Plus 1 Is The Sum Of The Series 1 2 3 Plus 2 3 4Let's note math(a/mathmath_n)_{n \in \mathbb N^*}/math the sequence Notice that math\displaystyle 1 \times 3 \times 5 \times \ldots \times (2n1)=\frac{1In zeta function regularization, the series ∑ = ∞ is replaced by the series ∑ = ∞ −The latter series is an example of a Dirichlet seriesWhen the real part of s is greater than 1, the Dirichlet series converges, and its sum is the Riemann zeta function ζ(s)On the other hand, the Dirichlet series diverges when the real part of s is less than or equal to 1, so, in particular, the



Mathematical Induction Online Presentation


Infinite Series Sum 1 N 1 N 1 3 5 2n 1 Convergence Using The Ratio Test Youtube
Mathoperators Share Improve this question Follow edited Sep 5 '15 at 2108 user asked Sep 5 '15 at 42 Shujian Ke Shujian Ke 43 1 1 silver badge 3 3 bronze badges 4 3Epic Collection of Mathematical Induction https//wwwmathgotservedcom/mathematicalinductionProve 1) 123n=n(n1)/2 htThe given series is {eq}\sum_{n=1}^{\infty }\frac{n!x^{n}}{135(2n1)}=\sum _{n=1}^{\infty \}\frac{n!x^n}{\left(2n1\right)!} {/eq} So, here we can apply the



Convergent Divergent Geometric Series With Manipulation Video Khan Academy


What Is The Sum Of The Series 1 1 3 5 1 3 5 7 1 5 7 9 Up To N Terms Quora
The next term of the sequence, ie the (n1)th term 1, 3, 5, , (2n1) which is summed is (2n1), now with n=1 the relationship, 1 3 5 (2n1) = n^2 (1) holds obviously since both sides are 1 Now say (1) holds for n = k for some positive integer k, then, 1 3 5 (2k1) = k^2 add the next term (2k1) to both sides, then;Express your answer as a fraction in simplest formOne can collect the terms in pairs (since the terms go to 0, this is okay) to get \begin{align} \sum_{n=1}^\infty\left(\frac1{2n1}\frac1{2n}\right) &=\sum_{n=1



Notes On Topics Of Algebra Notes



Mathematical Induction Sum Of Series 1 5 9 13 4n 3 N 2n 1 Youtube
Answer to 5 Question (3 Points) The sum of the series (1)" (37)2n1 is 22n1 (2n 1)!Our task is to create a program to find the sum of the series 1 (13) (135) (1357) (1357(2n1)) From this series, we can observe that ith term of the series is the sum of first i odd numbersOur task is to create a program to find the sum of the series 1 (13) (135) (1357) (1357(2n1)) From this series, we can observe that ith term of the series is the sum of first i odd numbers
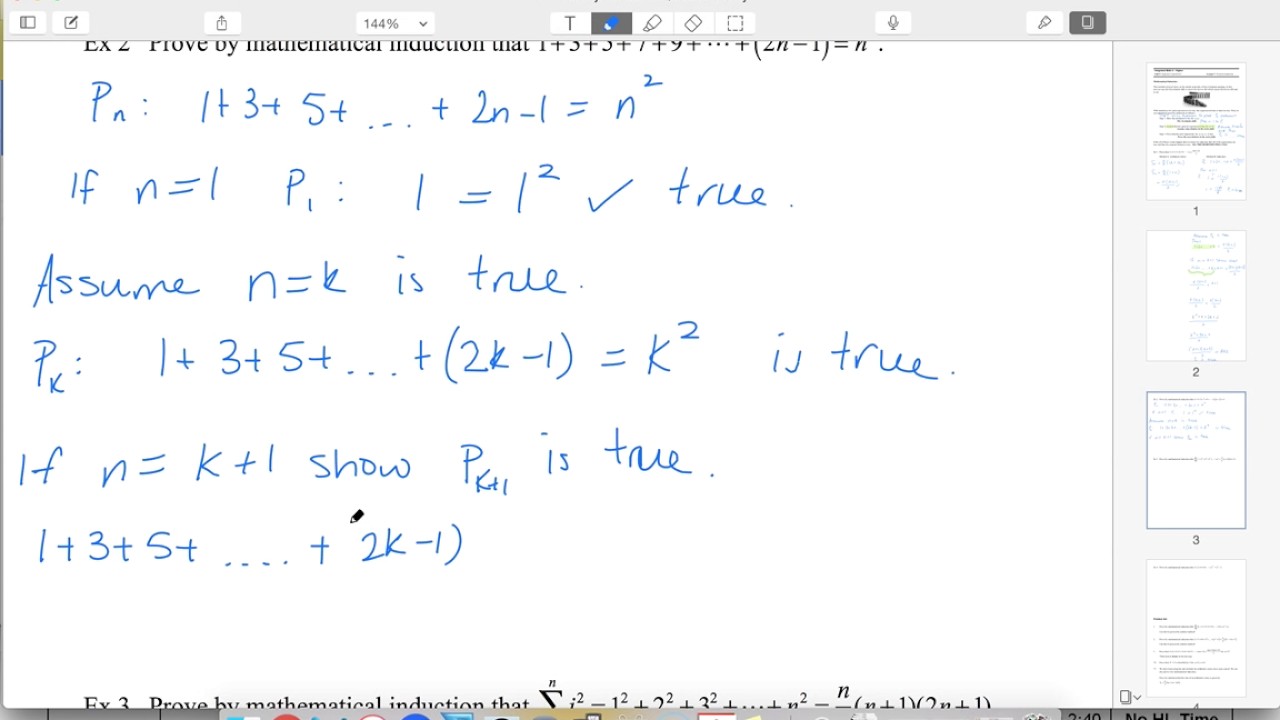


05 07 Ex2 Prove Sum Of First N Odd Numbers Is N 2 By Induction Youtube



Answered And N 2n 1 N 1 3 5 13 The Bartleby
Mathoperators Share Improve this question Follow edited Sep 5 '15 at 2108 user asked Sep 5 '15 at 42 Shujian Ke Shujian Ke 43 1 1 silver badge 3 3 bronze badges 4 3What is the value of the sum 1/1*3 1/3*5 1/5*7 1/7*91/199*1?1 3 5 (2n1) = ?



Find The General Term And The Sum Of N Terms Of The Series 3 1 1139 167



Preliminary To Math Induction An Infinite Sequence Of Propositions
Let mathf(x) = x^2/math Since, mathf(x)=(x)^2=x^2=f(x)/math Hence, mathf(x)/math is an even function Therefore, the Fourier series of mathf(x)/mathNow, if we subtract the second equation from the first, the 1/2, 1/4, 1/8, etc all cancel, and we get S (1/2)S = 1 which means S/2 = 1 and so S = 2 This same technique can be used to find the sum of any "geometric series", that it, a series where each term is some number r times the previous term2n1 − 1 F 2 = F 3 − F 1 F 4 = F 5 − F 3 F 6 = F 7 − F 5 F 8 = F 9 − F 7 F 2n−2 = F 2n−1 − F 2n−3 F 2n = F 2n1 − F 2n−1 Adding up all the terms on the left sides will give us something equal to the sum of the terms on the right sides



Find The Sum Of The First 2n Terms Of The Series 1 2 2 3 2 4 5 2 6 Brainly In


How To Sum 1 3 5 7 111 In C Programming Quora
Get an answer for '`sum_(n=1)^oo (2n^21)/(3n^52n1)` Use the Limit Comparison Test to determine the convergence or divergence of the series' and find homework help for other Math questions atA n = (1 3 5 7 (2n1)) = sum of first n odd numbers = n 2 Refer this post for the proof of above formula Now, Refer this post for the proof of above formula C filter_none edit close play_arrow link brightness_4 code // C implementation to find the sum // of the given series #includeInstructor So, we've got a Riemann sum We're gonna take the limit as N approaches infinity and the goal of this video is to see if we can rewrite this as a definite integral I encourage you to pause the video and see if you can work through it on your own So, let's remind ourselves how a definite integral can relate to a Riemann sum



Og 3 S Lo N3 2 Cos Kvk2 1 K 1 0o 7 Find The Exact Chegg Com


How To Prove That Math 1 3 3 3 5 3 2n 1 3 2n 4 N 2 Math Using Mathematical Induction Quora
The sum of the series n1 1 See answer yasjjoshi4760 is waiting for your help Add your answer and earn points Brainly User Brainly User There are n terms in the series Because last odd term =2n1 and rth odd term is denoted by 2r1 We can also calculate number of terms by formulaNow, if we subtract the second equation from the first, the 1/2, 1/4, 1/8, etc all cancel, and we get S (1/2)S = 1 which means S/2 = 1 and so S = 2 This same technique can be used to find the sum of any "geometric series", that it, a series where each term is some number r times the previous termWeekly Subscription $199 USD per week until cancelled Monthly Subscription $499 USD per month until cancelled Annual Subscription $2999 USD per year until cancelled



Find The Sum Of The Following Series Up To N Terms 1 3 1 1 3 2 3 1 3 1 3 2 3 3 3 1 3 5 Mathematics Shaalaa Com


Sum Of First N Odd Natural Numbers 1 3 5 2n 1 Summation Of First N Odd Numbers Youtube
Conjecture a formula for the sum 1/1 (3) 1/3 (5) 1/(2n1) (2n1)?Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeThis is an arithmetic series with a=1 and d=2 The Nth term is a(N1)d=12(N1)=2N1=2n1 so N=(n1) The sum is (N/2)(2a(N1)d)=N^2=(n1)^2 Check n=3, 1357=16=(31)^2 so OK



Sum Of N Squares Part 1 Video Khan Academy



Sequence Function
Find the sum of the terms of the arithmetic sequence 1, 7, 13, 19, , 109, n = 19 asked Feb 19, 14 in ALGEBRA 1 by johnkelly Apprentice sequenceseriesThis basically tells me that the arithmetic sequence is 2n1 To verify, simply plug in the 1st term (n=0) and you'll get 1 Plug in the 2nd term (n=1) you'll get 3, if I let n=2 I get 5, etc1 simple enough, create a new variable `num` and bind it to the number `1` 2 `num` is less than 10, so do the body of the loop 3 `num` is `1` so now bind it to `2` 4 create a new variable `mySum` and bind to `2` (same as num) 5 `mySum` is `2` and `num` is `2` so bind `mySum` to `4` Back to the top of the loop 2 `num` is less than 10, so



Solved R 1 1 2 3 2n 1 3 5 7 Cos X 1 Chegg Com



How To Evaluate The Sum Of N 2 N From N 1 To Infinity Quora
How to find the sum of a sequence, eg (2n 1)^3 How to find the sum of a sequence, eg (2 nJust make sure to use dot () as a decimal notation, eg 15 instead of 1,5 since the latter will be interpreted as two separate numbers, one and five, by our sum calculator In "Sigma notation" mode you are to enter the lower and upper limits, a mathematical expression through which each member of the sum series is to be computed, and finallyYou have to be very careful with power series They all have a range of values for which they work Consider the power series P = 1 x x^2 x^3 x^4 x^5 x^6 \pm \cdots This is a



Solved Let P N Be The Proposition That 135 2n 1 2 We Ca Chegg Com



Prove That 2n 1 N 2 N 1 3 5 2n 1 2n 1 Youtube
We can square n each time and sum the result 4 Σ n=1 n 2 = 1 2 2 2 3 2 4 2 = 30 We can add up the first four terms in the sequence 2n1 4(1) 1 3 5 57 Note that the sum of the first 2 odd positive integers = 2^2 And the sum of the first 3 positive odds = 3^2 And 2n 1 = 57View Notes hw1 from MATH 315 at University of Oregon Homework #1 14 (a) Guess a formula for 1 3 5 (2n 1) by evaluating the sum for n = 1, 2, 3, and 4 (b) Prove your formula using



Solved 3 Prove That 1 3 5 2n 1 N2 For Al Chegg Com



Solved Let P N Be The Proposition That 1 3 5 2n 1 N2 We Chegg Com
}\ \ }{ 1009\cdot 1345 } \\ \\ &=\frac {\ \ \frac { 17\cdot 18\cdot 4035 }{ 2\cdot 3 }\ \ }{ 1009\cdot 1345 } \\\\ &=\frac { 17\cdot 1009\cdot 1345 }{ 1009\cdot 1345 } \\ \\ &=17\ _\square \endN=1 2T 6 11 6 13 л 231 31 6 13 2 л1 Answer to Write a while loop fragment that calculates the following values (a) Sum of the first n counting numbers 1 2 3 n (b) Sum of the first n odd numbers 1 3 5 2n − 1 (c) Sum of a series of numbers entered by the user until the value 999 is entered Note 999 should



The A M Of 1 3 5 2n 1 Is


How To Evaluate The Sum Of N 2 2 N From N 1 To Infinity Quora
I want to use \sum to express 1 3 5 7 2n 1 Can I?The next term of the sequence, ie the (n1)th term 1, 3, 5, , (2n1) which is summed is (2n1), now with n=1 the relationship, 1 3 5 (2n1) = n^2 (1) holds obviously since both sides are 1 Now say (1) holds for n = k for some positive integer k, then, 1 3 5 (2k1) = k^2 add the next term (2k1) to both sides, then;



Maths Zone Sum Of First N Odd Numbers Is N 2 Facebook



Solved Problem 1 A Calculate 1 3 5 2n 1 For Several Chegg Com



Number Sequences Overhang This Lecture We Will Study Some Simple Number Sequences And Their Properties The Topics Include Representation Of A Sequence Ppt Download



Solved Write The Expanded Form Of Each Series 3 S N2 1 Chegg Com



Sum To N Terms 1 1 3 1 3 5 1 5 7 Youtube


What Is The Sum Of 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 95 97 99 Quora



Solved Evaluate The Sum Of The Following Series Summatio Chegg Com



Find The Sum Of Series Upto N Terms 2n 1 2n 1 3 2n 1 2n
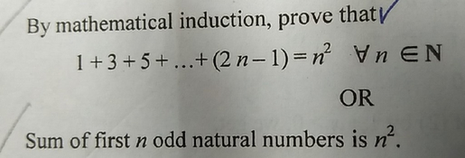


By Mathematical Induction Prove Thaty 1 3 5 2n 1 N2 Yn Scholr


What The Sum Of 1 1 2 1 3 2 1 5 2 1 2n 1 2 Quora



Chapter 10 Mathematical Induction People Vcu Edu



By Pmi Prove 1 1 3 1 3 5 1 5 7 1 2n 1 2n 1 N 2n 1 Brainly In



Grade 10 Math What The Frick Why Is The Sum Of This Arithmetic Series N 2 2n Homeworkhelp



Answered A Fill In The Blank 1 3 5 Bartleby



Sum Of Squares Of Odd Numbers 1 2 3 2 5 2 2n 1 2 Derivation Formula Prmo Rmo Iit Youtube



Solved Problem 1 A Calculate 1 3 5 2n 1 For Several Nat Chegg Com



Solved Write Out The Sum N 1 Sigma K 0 2k 3 5 7 9 Chegg Com



To Solve The Sum Of The Series 1 3 5 2n 1 Where K 1 To N Nth Term In The Series Graphically By Jimmy Lo Medium


Mple 2 17 Find The Sum Of The First 2n Terms Of The Followin Scholr



Solved Show That The Sum Sn Of The First N Terms Of The S Chegg Com



Sum The Series 1 3 7 15 31 To N Terms Brainly In



11 4 Series Sigma Notation Ppt Video Online Download



Find The Sum To N Term Of The Series 1 3 5 3 5 7 5 7 9



Find The Sum Of Series Upto N Terms 2n 1 2n 1 3 2n 1 2n 1 2 5 2n 1 2n 1 3 Youtube



Find The Sum Of The Series 2 3 5 9 8 15 11 21 To 2n 1 Terms Youtube



Find The Sum To N Terms 1 2 3 2 5 2 Youtube


How To Find The Sum Of The Series Math Frac 1 1 3 Frac 2 1 3 5 Frac 3 1 3 5 7 Frac 4 1 3 5 7 9 Math Quora



Solved Find The Sum Of The Series 1 1 3 1 3 5 1 5 7 Chegg Com



Solved Consider The Statement For All N E N 1 3 5 Chegg Com



Example 6 Show That Middle Term In Expansion Of 1 X 2n Is
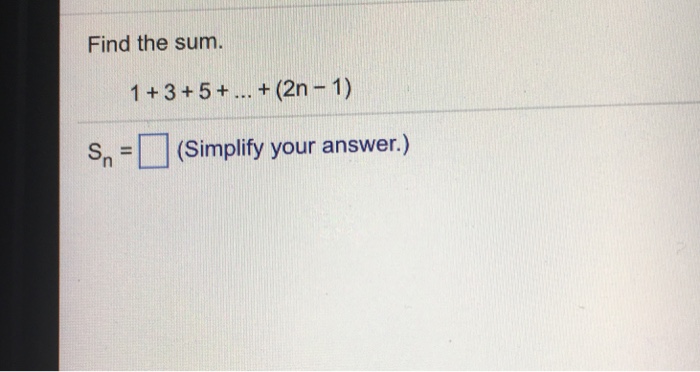


Solved Find The Sum 1 3 5 2n 1 Sn Simplify Yo Chegg Com



Illustration 19 Find The Sum Of N Terms Of The Series 1 3 5 3 5 7



Solved Usins Iiduclioln Verily Thal Cacil Eqtal Is Elor Chegg Com



Find Sum Of Series 1 3 5 7 9 11 Upto N Terms When Brainly In



Sum To N Terms 2n 1 2 2n 3 3 2n 5 Youtube



Let The Sequence 1 3 5 7 9 To 2n 1 Taken Show That Sum Of Alternate Terms 1 5 9 To The Brainly In



Solved Write The Sum In Sigma Notation 1 1 3 5 7 2n Chegg Com



Sum Of N Terms Of The Series 2n 1 2 2n 3 3 2n 5 Is



7 Proof By Induction 1 3 5 7 2n 1 N 2 Discrete Prove All N In N Induction Mathgotserved Youtube
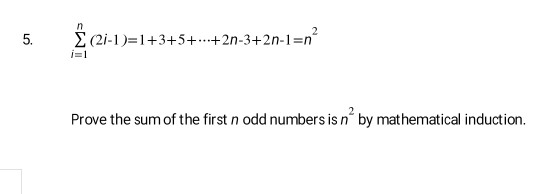


Solved 5 S 2i 1 1 3 5 2n 3 2n 1 N Prove The Sum O Chegg Com



Ex 9 4 10 Find Sum Of Series Nth Terms Is 2n 1 2 Ex 9 4



A Find The Am Of 1 3 5 2n 1 B Given Two Numbers A An



Example 5 By Mathematical Induction Prove That 1 3 5 2n 1



The Sum Of The Series Upto N Termsi To 1 1 3 1 3 5



Solved Write The Sum In Sigma Notation 1 3 5 7 Chegg Com



If The Nth Term Of An Ap Is 2n 1 Then The Sum Of Its First Three Terms Is Youtube



29 The Sum Of N Terms Of The Series11 1 Is 1 3 5 3 5 7 5 7 9


What Is The Value Of 1 3 1 5 1 7 1 49 Quora



Solved 2 Consider The Sum 1 3 5 7 2n 1 A Rewrite Us Chegg Com



Solved Q2 Induction For Each Integer N 2 1 Define The S Chegg Com



Find The Sum Of Series Upto N Terms 2n 1 2n 1 3 2n 1 2n



Find The Sum To N Terms Of Each Of The Series In Exercises 1 To 7 N Begin Array L L Text 1 1 Times 2



File The Sum Of The First N Odd Integers Is N 1 3 5 2n 1 N Gif Wikipedia



Ex 4 1 17 Prove 1 3 5 1 5 7 1 7 9 1 2n 1 2n 3



No comments:
Post a Comment